Cosa si cela dietro la perfezione assoluta della sequenza di Fibonacci


23 novembre, ovvero 23 11. Nella notazione americana della scrittura di una data, il mese anticipa il giorno: november 23, cioè 11 23, e ancora 1 1 2 3, scomponendo le singole cifre. Insomma, da una data particolare otteniamo dunque una sequenza di numeri ognuno dei quali rappresenta la somma dei due che lo precedono (immaginando ci sia uno zero in testa).
E’ ovvio che con questa regola semplice potremmo continuare all’infinito, non limitandoci alla sola scomposizione della data in questione:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987...
Questa successione di numeri viene storicamente legata alla soluzione di un problema proposto dall’Imperatore Federico II di Svevia nel 1223 durante un torneo matematico, a Pisa, e risolto in modo rapido e brillante da un matematico italiano, Leonardo Pisano, “figlio di Bonaccio” (filius Bonaccii), ovvero Fibonacci:
“Quante coppie di conigli si ottengono in un anno, salvo i casi di morte, supponendo che ogni coppia dia alla luce un’altra coppia ogni mese e che le coppie più giovani siano in grado di riprodursi già al secondo mese di vita?”
Cos’ha di così interessante questa successione, oltre a raccontarci la crescita delle coppie di conigli? Immaginiamo di costruire, partendo da questi numeri, una figura geometrica basata su una sequenza di quadrati, in modo che ogni nuovo quadrato abbia un lato di lunghezza pari alla somma dei lati dei due quadrati più vicini:
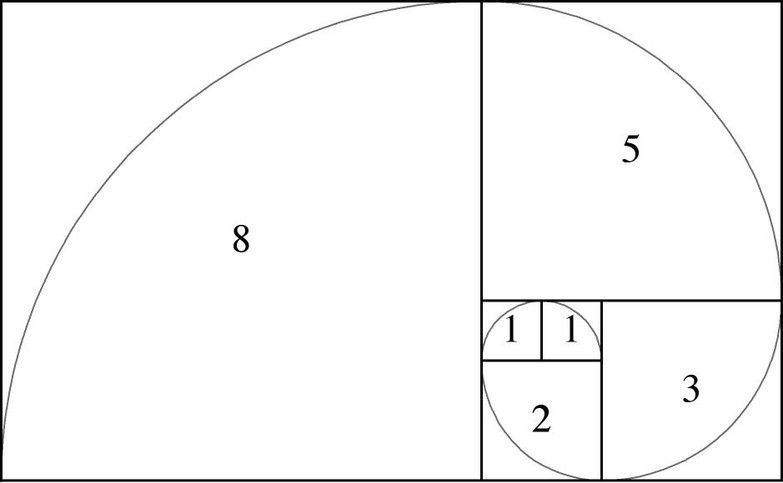
Inscrivendo un arco pari a un quarto di circonferenza in ciascuno di questi quadrati, si ottiene una spirale molto particolare, dotata di un “fattore di crescita” che è rappresentato da un altro numero straordinario, che apparentemente non sembrerebbe avere nulla a che fare con la successione di Fibonacci.
Sveliamo il mistero...
Prendiamo un segmento e dividiamolo in due parti diseguali, a e b, in modo tale che la parte più corta, b, risulti proporzionale alla più lunga, a, allo stesso modo in cui quest’ultima è proporzionale all’intero segmento (a + b):
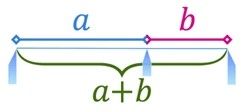
In questa proporzione così definita, il rapporto a/b è pari a 1.61803... un numero che ha infinite cifre decimali e che rappresenta la cosiddetta “sezione aurea”, indicata dalla lettera ϕ. Cos’ha di tanto particolare questo numero e qual è il suo legame con la successione di Fibonacci?
Chiamata anche “divina proporzione”, la sezione aurea è un rapporto ben conosciuto sin dall’antichità ed è considerato l’elemento che caratterizza al meglio l’equilibrio di certe forme. In parole povere, esso è associato all’idea di armonia, di bellezza, come possiamo osservare in molte opere d’arte e architettoniche (una su tutte, il Partenone). Anche nel corpo umano, molte sezioni e rapporti morfologici si collegano a questo numero (ad esempio, le parti di una mano). Addirittura è stato fatto notare che i rapporti migliori nei valori della pressione sanguigna si avvicinano a quello della sezione aurea!
Più in generale, è la Natura stessa che sembra “amare” in modo particolare questo numero straordinario, anzi, fondare molte delle sue forme sulla successione di Fibonacci.
È dunque arrivato il momento di svelare l’arcano: qual è il rapporto tra questa successione e la sezione aurea? Si può scoprire con facilità tramite una semplice divisione, quella fra gli elementi contigui della stessa successione, per esempio: 8/3, 13/8, 21/13, 34/21... 987/610... Provato? Bene, avrete scoperto che il rapporto fra questi numeri, crescendo nella sequenza, si avvicina sempre più a quello della sezione aurea!
Torniamo ora alla nostra spirale di Fig. 1 e scopriamo che il suo fattore di crescita è proprio ϕ, la sezione aurea. Questo giustifica il suo nome di “spirale aurea”.

Qui sopra alcuni esempi di dove sia possibile “rintracciare” la successione di Fibonacci in Natura. Ecco quindi cos’hanno in comune la disposizione delle foglie lungo un fusto (fillotassi), gli uragani, le galassie... e così via!
C’è qualcosa di più e forse di più profondo... In questa sezione di articoli, abbiamo parlato più volte delle quattro forze fondamentali con le quali è possibile spiegare ogni cosa avvenga nell’universo (a parte ciò che ancora ha bisogno di una spiegazione!). Una di queste è la forza elettromagnetica, la cui intensità è centotrentasette volte più piccola di quella che tiene unito il nucleo e che garantisce l’esistenza della materia, la forza nucleare.
La costante adimensionale che rapporta l’intensità della forza elettromagnetica a quella nucleare viene chiamata “costante di struttura fine” (indicata con la lettera α), che vale appunto (2014 NIST CODATA, struttura che fornisce i valori “ufficiali” delle costanti fisico‒chimiche):
α = 1/137.035999139(31) = 7.2973525664(17)·10–3
(i numeri in parentesi, sommati o sottratti agli ultimi due numeri che sono ad essi adiacenti,
rappresentano l’intervallo di incertezza del valore)
La forza elettromagnetica da sola potrebbe spiegare l’esistenza di ogni cosa, compresa la nostra stessa presenza. Se fosse anche e solo di pochissimo differente, l’universo sarebbe qualcosa di completamente diverso. Forse nemmeno potrebbe contemplarci.
Alcuni anni fa, mi dedicai allo sviluppo di un’idea originale che produsse un risultato inatteso e sorprendente. Dallo sviluppo di un’equazione (detta differenziale perché l’incognita da trovare non è un numero ma una funzione o una famiglia di funzioni) sbucò fuori una costante che era proprio la sezione aurea. Approfondii allora l’elaborazione e scoprii che il logaritmo naturale della sezione aurea elevata al quadrato (che indicai col simbolo k) era strettamente correlato alla costante di struttura fine α tramite una relazione che sottintende una certa ricorsività, segno forse di un ordine sottostante, non ancora individuato. Il valore calcolato che la relazione tra sezione aurea e costante di struttura fine attribuisce a quest’ultima è:
αcalc = 7.2973525681·10–3
che rientra perfettamente nell’intervallo di incertezza del valore ufficiale riportato più sopra.
Si tratta solo di un caso? E se così non fosse? L’aspetto più interessante di questo sviluppo è che a partire da una costante puramente geometrica, matematica, derivabile da una successione di numeri su cui anche la Natura fonda alcune sue forme, si può derivare una costante che è ottenuta dal rapporto di costanti fisiche ‒ che descrivono il mondo fisico, il mondo reale ‒ in una sorta di passaggio figurato dall’inanimato all’animato. È un altro dei segnali che, partendo da Fibonacci e dalla sezione aurea, cercano di suggerirci che al fondo ultimo della realtà ci sia... il Numero? O è solo l’ossessione per la ricerca della Bellezza?
Appuntamento allora al prossimo 23 novembre con i numeri del Fibonacci Day, anche se temo che questa data verrà dimenticata a favore dei più chiassosi numeri sugli incassi del Black Friday!
Per chi abbia familiarità con la matematica, l’espressione da me trovata, che fornisce il valore calcolato della costante di struttura fine α (l’incognita!) in relazione alla sezione aurea ϕ tramite la posizione k ≡ ln (ϕ2), è questa:
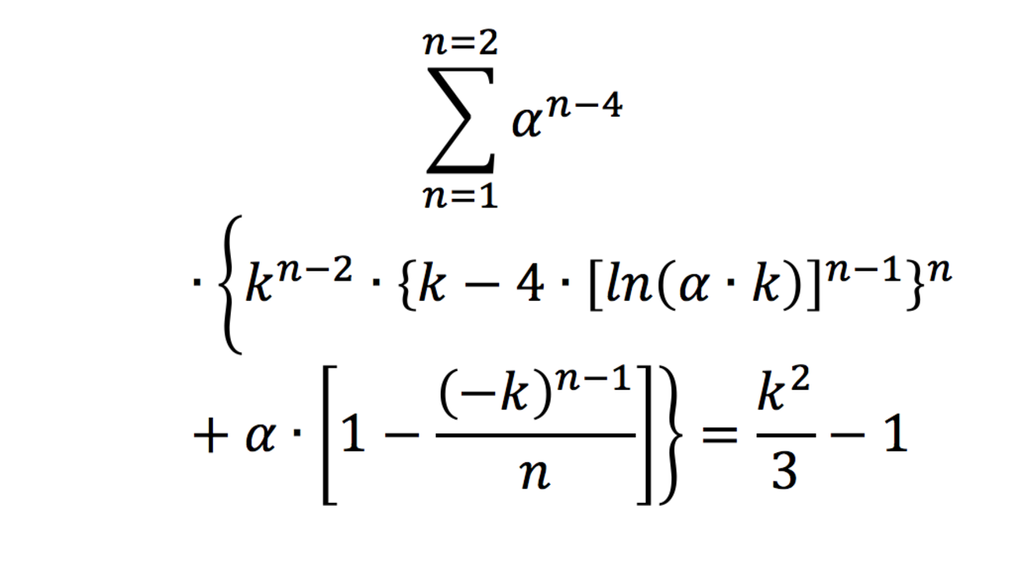
Un’ultima curiosità. La storia di questa “scoperta” e dell’ossessione per la ricerca della Bellezza è stata romanzata nel libro “Se questo è l’infinito” (Youcanprint).